写真でも絵画でも、何かを作ろうとする時にはどんな表現が正解なのか迷います。
主題の決定、使う技法、ロケーション、光の入れ方、構図。
多くの要素についてそれぞれ最も良いものを考えるのは大変な作業です。
しかし、構図の取り方についてだけは、よく言われる正解の一つとして「黄金比」があります。
では黄金比の構図ってどういうことでしょうか。
Twitterでも黄金比や白銀比が話題になっていたのですが、最近ネットで出回っている黄金比の画面構成の概念がずいぶんお手軽になっていると感じました。
もっともらしく黄金比を当てはめてるけどそんな簡単なものじゃない、それは黄金比関係ない、と感じるものがほとんどです。
ちゃんとした黄金比の説明を調べてみましたが、黄金比の構図の代表的存在であるルネサンス期の絵画を、黄金比の観点で説明しているサイトが意外に存在しないのでゆるーく書いてみようと思います。
長くなるのでページを分けました。
黄金比はもう知ってるという人は直接説明ページを見てください。
黄金比って何?どこが特別?
ちなみに黄金比とは約1:1.618、白銀比は約1:1.414になる比率の事です。
美しい比率が黄金比ではありません。特殊な性質持つ一定の比率というだけです。
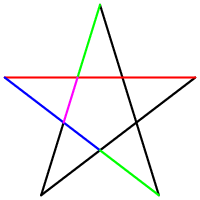
この比率の何が特別かというと、黄金比は同じ比率を延々と続けていくことができる点です。例えば右図において、青の線分と赤の線分の長さの比、同じく緑と青の比、紫と緑の比は一定の値![]() を取ります。
を取ります。
参考:Wikipedia
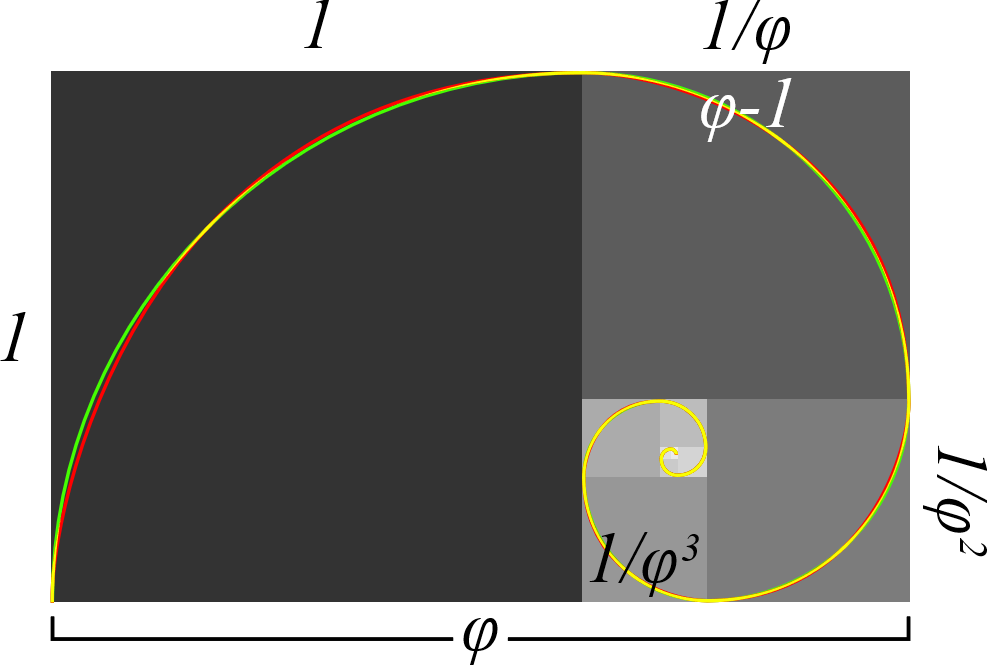
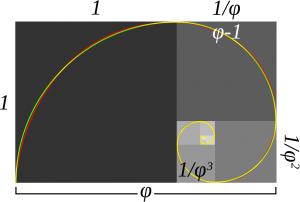
次の図の黒い方、螺旋が描かれた形を見てみましょう。
これは辺の比が黄金比になる長方形「黄金矩形 – おうごんくけい」です。
次の図のように黄金比の辺を持つ長方形から黒の部分の正方形を引くと、右側のグレー部分のようにまた元と同じ形の長方形が残ります。
この残った長方形は元の長方形を同じ比率であり、相似します。
ここからまた正方形を引くと、また相似の長方形が現れるというように延々と繰り返します。
他にも黄金比に関わる興味深い話としてフィボナッチ数列という数列があります。
この数の特性は0+1=1 1+1=2 1+2=3 2+3=5 5+8=13 という、2つの数字の和とその前の数を足し算していくと次の数字になるというもの。
数学が苦手な私には数列は詳しく説明できませんが、この特殊なフィボナッチ数を辺の長さとした正方形を重ねていくと、黄金比に近くなります。

今までの説明でピンと来ない人のために、特別な比率について身近にあるわかりやすい例を出してみます。
普段よく使うA4の紙にも特殊な比率が含まれます。
A4紙は黄金比ではないのですが、白銀比と言われています。
A4の紙を二つに折るとA5になり、さらに二つに折ればA6になる便利な比率です。
「同じ比率を繰り返す」というのが黄金比や白銀比が特別な理由です。
黄金比は美しさよりも神秘を象徴するためのもの?
黄金比とはこのように特殊な性質を持つため、神秘的な数字とされていました。
絵画には見た目だけではわらかない隠されたメッセージが様々な象徴にこめられています。
そのメッセージは今日では図像解釈学(イコノロジー)という学問によって体系づけられていますが、神の奇跡を描く宗教画において、より深く奇跡の場面を表現するには黄金比のような特別な比率で奇跡を象徴し、演出することが不可欠だったのでしょう。
黄金比とは美しさの象徴ではなく、神秘を表現する手段と考えた方が良いかもしれません。
以上が黄金比の基本的な説明でした。
2回に分けて書きますが、次はティントレットの絵画を参考にして黄金比構図を説明します。
ティントレットの絵画に隠れた黄金比構図の説明





No comment yet, add your voice below!