写真や絵画において色々な構図の取り方があります。
この記事では構図の取り方の1つである黄金比について書いてみました。
黄金比を使った構図の説明サイトは色々とあるのですが、ネットでの流行のせいか写真での黄金比構図の説明サイトばかりを見かけます。
もっともらしく黄金比を当てはめてるけどそんな簡単なものじゃない、それは黄金比関係ない、と感じるものがほとんどです。
元々の黄金比の構図について書かずにはいられなくなりました。
長くなりますがお付き合いください。
そもそも黄金比って何?という方は下のリンクから前の記事「黄金比とは」を参照してください。
そんな事を踏まえつつ、黄金比の画面とは何かを解説します。
解説にあたり、雑誌美術の窓を参考にしています。
(「黄金比による構図」,『美術の窓』2003年3月号, p.32-33,生活の友社.)
黄金比の前にこの絵画について簡単に説明

この絵はルネサンス期の画家ティントレットによる「青銅の蛇」です。
この時代は宗教画や物語画と言われる聖書や神話の内容を視覚化したものが絵画の主流でした。
文字を読むことができない人がほとんどであった時代、宗教画は聖書を人々に図で説明するという役割もありました。
このティントレットの絵も旧約聖書における場面を描いたものです。
イスラエルの民がモーセに導かれ約束の地カナンを目指す途中、旅の厳しさによって不平が募り主を冒涜するような言動が発せられるようになりました。
主は彼らを懲らしめるために炎の毒蛇を地上に送り、多くの人がそれに噛まれて死にました。
罪を悔いた人々はモーセに蛇を取り去るよう主に祈ってほしいと願います。
主はモーセの祈りに応え、モーセは主の言葉通りに青銅で蛇を作り、竿の上に架けました。
蛇に噛まれた人々もこの青銅の蛇を見上げると命が助かりました。
さぁ黄金比の説明です
さて前置きが長くなりましたが、この絵画では黄金比がたくさん活用されています。
ここまで予定よりずいぶん長く書いてしまったので、できるだけ短く書きます。
この絵の縦、横の比率はほぼ黄金比の長方形「黄金矩形」です。
この絵をパっと見た感じでは上に三角っぽい塊があり、下にもちょっと歪な三角がある、と思った人がいるかもしれません。
しかし、この歪にも見える不等辺三角形はしっかりと計算された図形に沿っています。

図は黄金矩形から正方形を取り、正方形と矩形に分けています。
正方形の残りでできた矩形は元の画面の相似となり、この相似の矩形からまた正方形を取ると、残りの矩形はまた相似します。
図のSBCS1は正方形で、残りのASS1Dの矩形は黄金比の相似矩形になります。
同じ要領で残った矩形ASS1Dから正方形を取り、さらに残った形から正方形を取る作業を繰り返します。
見事に正方形と相似矩形が繰り返されました。
この画面は上下に2分割され、中央には空を仰ぐイスラエルの民が見えます。
さらに全体から正方形を取った点SS1には神に祈るモーセの姿が見えます。
上部の黄金矩形には神と天使の塊があり、下部の正方形には蛇に噛まれた人々(罰を受けたイスラエルの民)の塊が見えます。
画面下にある人の塊は画面左下のBと画面右のS5をつないだ点と、画面右下Cと画面中央S3をつないだ点に沿った三角形に一致します。
画面下の不等辺三角形は計算して生まれた形でした。
また、画面上部の天上の神と天使の姿は黄金矩形に納まり、神の広げた手はS2S5の辺に沿い、その体はS2S4S5の二等辺三角形に納まります。
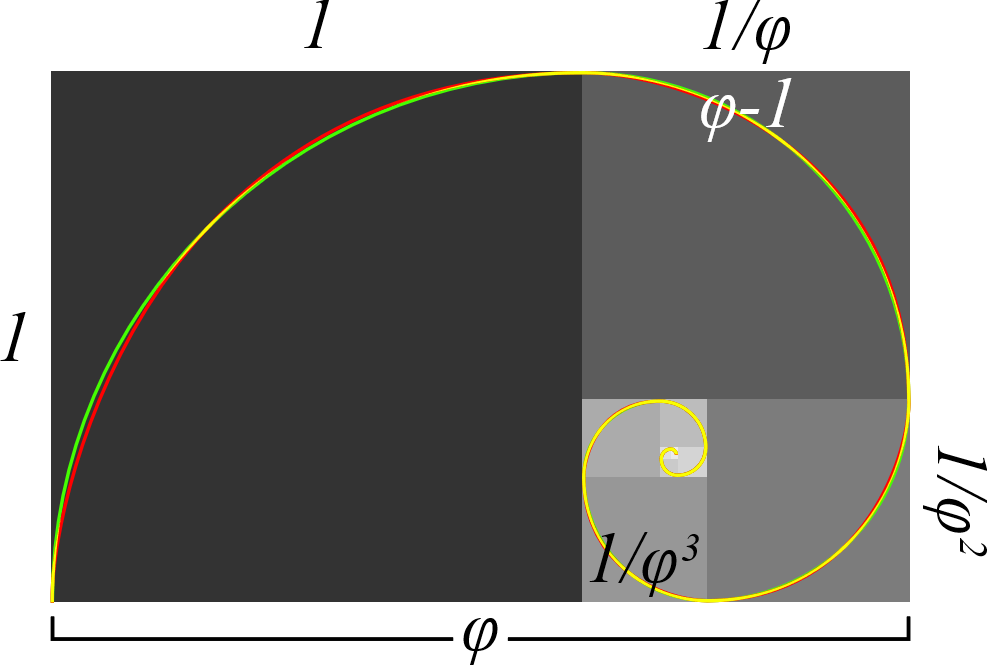
よく見る黄金比の説明図、黄金螺旋

こちらは各点を曲線でつないだ黄金螺旋です。
黄金比の説明ではこの螺旋をよく目にしますが、この螺旋を使うことだけが黄金比の画面構成ではありません。
とはいえ、やはりこの螺旋形を使うと黄金比の動きがわかりやすくなります。
正方形との分割画面ほどではありませんが、この螺旋に沿って人の塊の中でも目立つ部分や天上で影になった天使達が配置されていきます。
結局黄金比を使った画面が正解なのか
いくつもある美の理論において、黄金比ほど有名なものはないと思います。
しかし、これが美しさの正解かというと、そうとも言い切れません。
美しいと感じるのは人それぞれであり、国や文化で変わります。
ティントレットの絵のように、ルネサンス期の絵画は非常に計算され尽くした画面構成で描かれました。
均衡の取れた画面ではありますが、理論的すぎて面白味に欠けています。
ルネサンスが過ぎ、やがて時代はダイナミックな表現を求めてバロックの時代を迎えます。
カラヴァッジョやルーベンスに代表される光と影、躍動感ある動きが絵画で表現されていきます。
バロックとは真珠や宝石のいびつな形を指すポルトガル語のbarrocoから来ていると言われますが、ルネサンスでやり尽くされた計算された絵画を崩すことで絵画表現をさらに発展させました。
バロックの絵画からも黄金比が見て取れるものはたくさんありますが、黄金比から抜け出すことで独創的な表現が成立します。
写真における黄金比と構図
最後に。
最近写真においても黄金比を意識するという話をよく見るのですが、だいたいは黄金比関係ないんじゃないかって思ってます。
本来の黄金比を意識した画面というのは複雑なものです。
画面を計算して分割できる絵画やデザインとは異なり、現実世界にあるものを切り取る写真ではこのような黄金比に沿った画面構成というのは不可能です。
できてもある程度の比率や動きのリズムを黄金比に似せる程度でしょう。
と思ってたけどこちらのサイトでは結構黄金比に沿った構図が載っていました。
たしかにこのくらいの使い方はできるかもしれませんが、黄金比が美しいと言われてきた根拠の絵画とはかなり密度が異なります。
このシンプルな黄金比は毎回意識していると似たような構図ばかりになってしまうことでしょう。
では写真における構図法とは何か。
Twitterで相互フォローさせていただいているよしーさんがとても良いまとめを出していました。
有名なところで三分割法などがありますが、写真で意識できる構図法とはこのようなものでしょう。
画面を三分割する、三角にする、斜めにするなど。
構図に迷うのであればまず黄金比一択ではなく、これらを覚えてみることから始めると良いかもしれません。
もちろん慣れてきたら自分だけの撮り方を考えなくてはいけないので、結局はこれさえあれば良いという正解なんてない、というのが答えになってしまいそうです。
構図についてはもう一つ参考のサイトをリンクしておきます。
ここまで黄金比について書いておきながら、タイトルにもある白銀比には触れていませんでした。
白銀比というのは美術史上、意識された言葉や概念ではなかったと思われます。
偶然名画の画面がその比率になることはあったかもしれませんが、個人的には白銀比での画面構成が美しいというのは後付けで、根拠を持ってこれが美の法則だ!と説明するには無理があると思います。
便利な比率だとは思うけど、それが美しいとは限らないってこと。
一通り書いてみたら全然ゆるくない長さでした。